皆さんは「微分」の正しい定義をご存知ですか?
「おいおい、舐めるんじゃないよ。ただ次数を下げれば良いと思っている人たちとは違うぜ。」
そんな声が聞こえてきそうです。今回はそんな「微分」の定義についてのお話。数学という学問は、つくづく「隙がない」なぁと、そう感じずにはいられない内容です。では、参りましょう。
平均変化率から導関数まで

詳しい話をする前に、高校生の数学Ⅱの「微分法」の単元で学ぶ、基本的な事柄を確認していきましょう。まずは学校の教科書に習って、「平均変化率」から出発し「導関数」までを定義していきましょう。
平均変化率の定義
関数\(y=f(x)\)において、\(x\)の値が\(a\)から\(b\)まで変化するとき、\(y\)の変化量\(f(b)-f(a)\)の\(x\)の変化量に対する割合
$$\frac{f(b) – f(a)}{b – a}$$
を、\(x\)が\(a\)から\(b\)まで変化するときの関数\(f(x)\)の平均変化率という。
中学数学では「変化の割合」として学んでいたものを、ちゃんと\(f(x)\)という関数の表記の仕方を使って改めて定義した、という感じですね。
では次に、平均変化率と併せて極限の考え方を用いて「微分係数」を定義していきます。
微分係数の定義
平均変化率の式において、\(a\)を固定して、\(b\)を\(a\)に限りなく近づけた際、この割合がある一定の値\(\alpha\)に近づくとき(極限値\(\alpha\)が存在するとき)、この\(\alpha\)を関数\(f(x)\)の\(x=a\)における微分係数といい、\(f'(a)\)と表す。\(\lim\)の記号を使って表すと、次のようになる:
$$f'(a) = \lim_{b \to a} \frac{f(b) – f(a)}{b – a} = \lim_{h \to 0} \frac{f(a + h) – f(a)}{h}$$
ここまではよろしいでしょうか?
では次に、この微分係数を\(x\)の全体に拡張して「導関数」も定義してしまいましょう。
導関数の定義(微分する)
関数\(y = f(x)\)において、\(x\)の各値\(a\)に対して微分係数\(f'(a)\)を対応させて得られる関数を、関数\(f(x)\)の導関数といい、\(f'(x)\)で表す。極限の記号\(\lim\)を使って、導関数は次のように表される:
$$f'(x) = \lim_{h \to 0} \frac{f(x + h) – f(x)}{h}$$
また、関数\(f(x)\)の導関数\(f'(x)\)を求めることを、関数\(f(x)\)を微分するという。
「微分する」の定義はしましたが…
数学Ⅱの微分法の単元で学ぶ内容を、ざっとおさらいしていきました。(極限の定義については、今回は詳しくは触れないこととします。が、本当は厳密性が求められる、ということを添えておきます。)
ここで改めて皆さんに問いたいと思います。
皆さんは「微分」の正しい定義をご存知ですか?
さて、基本的な定義を一通り確認したわけですが、残念ながら上記の中に「微分」の定義はありません。
「え、導関数を求めることを微分するって言ってるじゃん!」
確かに言っています。しかしその定義は、微分「する」の定義でしかないのです。「微分する」は動詞であって、「微分」は名詞。もちろん両者に深い関係はあるのですが、実は単に「微分」と言われたときには、上記のような導関数を求める操作のことを指しているのではないのです。では、その定義とは何なのか。次で詳しくみていきましょう。
本当の「微分」の定義とは

では、本題に入りましょう。「微分」の真の定義は次のようなものです。
微分の定義
関数\(y = f(x)\)が微分可能であるとする。このとき、変数\(x\)が\(x\)から微小量\(\Delta x\)だけ増加した時の\(y\)の増分
$$\Delta y = f(x + \Delta x) – f(x) = f'(x)\Delta x + o(|\Delta x|)$$
の主要部\(f'(x)\Delta x\)を\(y\)の微分と呼び、\(dy\)と書く。
もし\(f(x) = x\)であれば、
$$dx = f'(x) \Delta x = 1 \cdot \Delta x = \Delta x$$
となる。これを用いて\(dy\)の定義を書き直せば,
$$dy = f'(x) dx$$
となる。
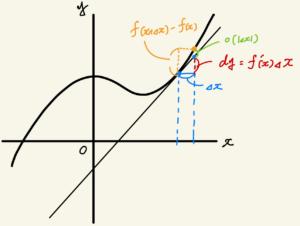
(ここで出てきた\(o(|\Delta x|)\)というのは「ランダウの記号」というもので、式全体への影響度が小さい\(\Delta x\)に関係する項を集めました!という意味です。影響度が小さいので、まとめて無視してしまいます。詳細はまたどこかで。)
一番衝撃なのが、「微分」の定義の中にすでに「微分可能」という言葉や導関数が登場していることですね。歴史的な背景としては、先に微分法という概念(考え方)が登場して、その際に用いていた\(f'(x)\Delta x\)などの増分(の主要部)に対して、後から名前を付けた、ということなのだと考えられます。
上記の数学的定義を理解することも重要ですが、大まかなイメージをお伝えするならば、関数の「微分」とは、変数が微小に増加した際の関数の微小な増分のこと、なんですね。
そうだったのか!用語の意味
ちなみに、初めの方で定義した「微分係数」。一体何の「係数」なのでしょうか?微分の定義の最後の式を見れば、\(f'(x)\)は微分\(dx\)の係数になっているので、\(x\)における微分係数と呼ぶことにも納得がいきます。
さらに、導関数や微分係数のことを「微分商」と呼ぶことがあります。これに関しても、先ほどの式を式変形をすれば
$$\frac{dy}{dx} = f'(x)$$
となっているので、微分商と呼ぶのも納得ですね。
まとめ
今回は「微分」という用語の正しい定義について解説してきました。これを知り、色々と調べたときに思ったことがあります。それは「学校の教科書って、よくできてるなぁ」ということです。(もし数Ⅱの教科書をお持ちであれば、調べてみてください。「微分」という言葉は単体では決して使われていないはずです。)
中学、高校で学ぶ数学は、広大な数学という世界のほんの一部でしかありません。時間や内容にも制約があるため、細かな議論を非常に上手に躱しています。今回の記事で少しでも「なるほど!」と感じたり、「そういえばあれって…」と思うことがあった方は、もうすぐ数学の厳密さの虜になってしまうかもしれませんね。
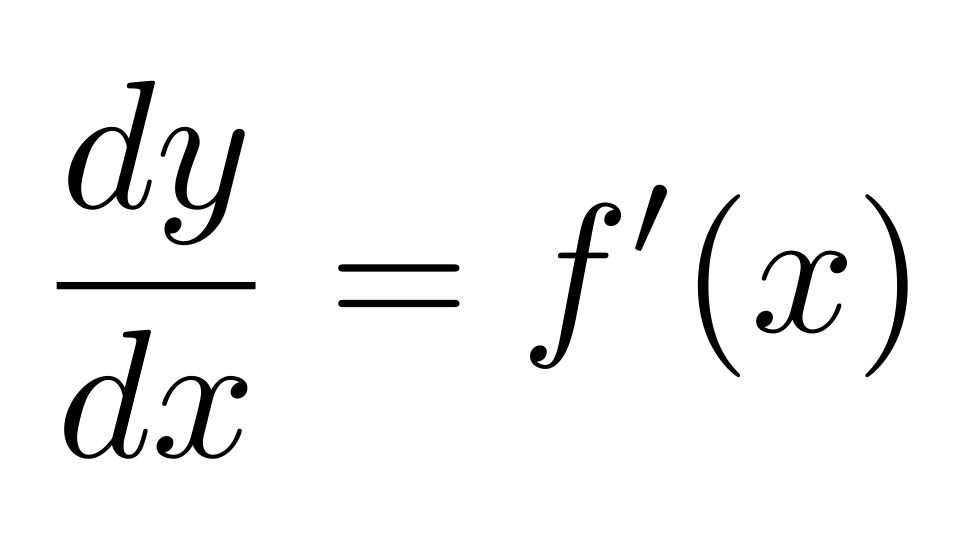


コメント