微積分とは
高校数学にて最後の礎と言っていい程の難関ですね。昔の生徒も非常に毛嫌いしていました。かく言う僕も専攻するまでは何一つ知らなく、大学で学ぶと微積分とは実に奥深いものでした。
ここでは、「微積分の美しさ・奥深さ」をお伝えしたい訳ではなく、「学ぶ意味」・「微積分の正体」をお伝えできればと思っています。（もちろん高校数学の範囲で）
微分とは 〜「微」を「分」ける〜
微分と聞いて、他の人にどのように説明するでしょうか。
次数を1つ下げて、指数を係数にする！
$$x^3 → 3x^2$$
大正解です！！
計算方法としては、高校数学の範囲では大正解です！！
しかし、それでこの章が終わってしまったら、この微分を取り上げている意味もないので、教科書にもある定義から「微分」を説明できればと思います。
まず、漢字であるように「微分」とは「微」々たるものに「分」けるということですね。
では、何を分けていくのでしょうか。
分けていくものは、「関数」です。
関数？？となる方もいらっしゃると思います。関数は、簡単に言ったら未来予測に役立つものなのです。
？？？？
まだまだ抽象度が高く、わかりにくい！との声が聞こえますので、具体例を上げていきます。
さて、質問です。
「中学生の時、身長は1年間に何cm伸びましたか？」
・・・・・
「5cm」
続いて質問です。
「中学生の時、身長は1ヶ月間に何cm伸びましたか？」
・・・・？？（やば、わからへん。。。）
「1cmぐらいかな」
さらに続けます。
「中学生の時、身長は1秒間に何cm伸びましたか？」
・・・・・！？？？（意味分からんなー分かるわけ無いやん）
「わかりません」
その通りですね(笑)
分かる人のほうが珍しいかと思います。
1年間という大きな間で変化ではなく、1秒間という短い期間での変化を考えることが「微分」ということです。
簡単に言えば、1年間の身長の伸び方（関数と思ってください）を非常に短いスパン（微小区間といいます）で分けて、どれぐらい伸びているのか（変化率といいます）を調べることです。
用語を使うと、
ある関数の変化率を微小区間で考える
という風になります。少しわかりにくいですね。
具体例と一緒に理解してくれれば、いいかと思います。
積分とは 〜「分」割されたものを「積」む〜
次は積分についてです。
高校数学の範囲では、数学Ⅲで習う内容になりますが、区分求積法でご説明できればと思います。
積分とは、簡単に言えば「面積を小さい長方形」に分けて、積み重ねたものになります。
ところで
「え、積分は微分の逆なのでは？」
と習った方も多い方と思います。そこについては非常に面白い内容となっておりますので、また別の機会にできればと思います。
なので今回は積み重ねていこうと思います。笑
簡単に積分の手順は以下のとおりです。
step.1 積分したい部分を長方形に分割する
step.2 分割した長方形の総和を求める
step.3 分割した横（縦）の長さを極限まで小さくする
具体的に、次のような積分について考えていきたいと思います。
$$\int_0^1 x^2 dx $$
step.1 積分したい部分を長方形に分割する
この積分を図形的に解釈すると以下の図なります。
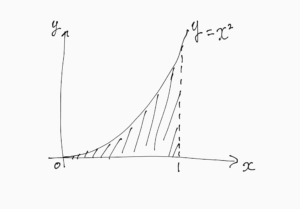斜線部が積分結果になります。この部分が、長方形に分割したい部分になります。
先に積分の計算を行いたいと思います。（ここでは微分計算の逆と思ってください。）
$$\int_0^1 x^2 dx = \frac{1}{3}$$
さて、ここからは長方形に分けて上記のような式になることを導いていこうと思います。
以下のような図をイメージしていただければと思います。
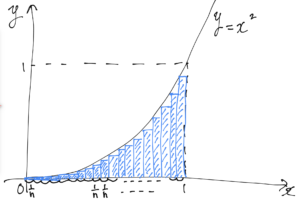
上記のように積分区間（x軸上の0から1の部分です）をn分割し、長方形を作ります。（青色の部分です）
step.2 分割した長方形の総和を求める
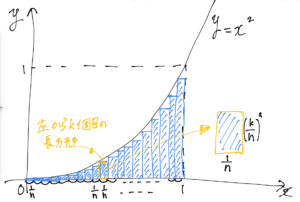
左からk番目の長方形（黄色の部分）を考えることで、1番目からn番目の長方形の面積を求めることができます。
k番目の長方形の面積は、縦×横になるので面積は
$$ 縦×横=\frac{1}{n}×(\frac{k}{n} )^2 $$
となります。
縦の長さは、関数 y=x^2 に x=k/n を代入して求めることができます。
また、x座標は長方形の左から数えていくとk番目に当たるので、k/nになります。
先程の黄色の長方形をk=1,2,・・・,nのときを全て足算します。
$$ \frac{1}{n}×(\frac{1}{n} )^2+\frac{1}{n}×(\frac{2}{n} )^2+・・・+\frac{1}{n}×(\frac{n-1}{n} )^2+\frac{1}{n}×(\frac{n}{n} )^2 $$
頭が痛くなるような数式ですね。笑
このような数式を、∑記号を用いて簡単に表したいと思います。
$$ \sum_{k=1}^{n} \frac{1}{n}(\frac{k}{n} )^2 $$
数列のΣ計算を行うと、
$$ \sum_{k=1}^{n} \frac{1}{n}(\frac{k}{n} )^2 = \frac{1}{n^3} \frac{n(n+1)(2n+1)}{6}$$
となります。
少し懐かしい計算でしたかね。もしわからない場合は、気軽に連絡くださいね。
twitter：@marieer1192
step.3 分割した横（縦）の長さを極限まで小さくする
そもそも、なんで横（縦）の長さを極限まで小さくするのでしょうか。
そんなこと言われても。。。。。
そうですよね。僕も唐突に聞かれても困ります。笑
理由をきちんと説明していきます。
結論から言うと、長方形の足算のみだと、以下の図のような誤差が生じるからです。
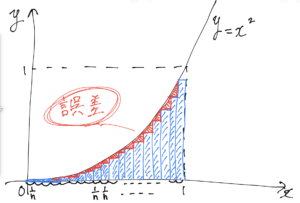
赤い部分が誤差になります。
この誤差をなくすために横の長さを極限まで小さくします。（今回は横の長さになります。縦の長さの場合もあるのですが、高校レベルでは殆ど出てきませんので、省略させていただきます。）
それでは、横の長さを極限まで小さくしたら誤差は減るのでしょうか。
以下の図を見てみてください。
赤で囲まれた部分が元々の誤差。一方で黄色の部分が小さくした場合に誤差になります。
図にしてもらえれば一目瞭然かと思います。
この時、次のように長さを定義します。
小＝dx
この様に定義すると、長方形の面積は
$$(\frac{k}{n})^2×dx$$
となります。k ではなく、xで書き換えると
$$ \frac{k}{n}=x → x^2×dx$$
となります。これを積み重ねるという意味で積分記号を使うと、次のように表すことができます。
$$ \int_0^1 x^2 dx $$
最終的に一番最初の形になりましたね。
インテグラルという記号は実は∑との関連性があるということがここで大切なことになります。
まとめ
今回の微積分で頭に入れていただきたいことは次の3つです。
① 微分は「変化率」→どれだけ変わったか
② 積分は「長方形を積み重ねる」→積分は足算と似ている
③ 微分と積分は必ず逆になるとは限らないこと
（今後説明させていただきます。）
今回は導入版となりましたが、次は「学習する意味」・「微分と積分の関係」についてお伝えできればと思います。
コメント